Akademiets forside | Opgaver til lektion 3 | Video til lektion 3 – del 1 |  Video til lektion 3 – del 2  | Video til lektion 3 – del 3 | Lektion 4

 

Backgammon Akademiet

Lektion 3:
introduktion til sandsynligheder

 

Vi kender det alle. Af og til er der en slags magi bag eller forbandelse over terningerne. Gang på gang kan vi ikke ramme, når modstanderen giver skud, og langt oftere bliver vi selv ramt. Eller vi kan ikke komme ind med en brik fra baren, mens modstanderen kommer ind med det samme. Det sker, og der er en del af spillet. Tilfældigheder råder, og det kræver stærke nerver at bevare det gode humør.

Men hvis det sker lidt for ofte, er der måske en anden forklaring end den rene tilfældighed eller ”uheld”. På langt sigt findes der hverken held eller uheld. Terningerne er tilfældige. Der er kun dygtighed til forskel. Så følger du dig forfulgt af uheld, så læs med her.

I backgammon er der to situationer, hvor det er vigtigt at have styr på sandsynlighederne. Den ene situation er den, hvor det gælder om at anbringe sine brikker på en måde, så man har størst mulig sandsynlighed for at udføre en bestemt opgave i næste rul, fx at dække en løs brik eller bringe den i sikkerhed. Den anden situation er den, hvor vi overvejer at doble eller at tage en dobling, og hvor vi har brug for at kende sandsynligheden for et bestemt udfald i næste rul. Disse situationer optræder tit, så det er ganske ofte, at vi har brug for at kunne beregne nogle bestemte sandsynligheder.

 

Simple sandsynligheder

 

Figur 1

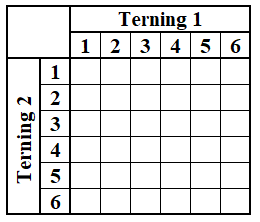
I backgammon kaster vi med 2 terninger med hver 6 sider. Antager vi, at terningerne er nøjagtig ens og præcist afbalancerede, kan vi udregne sandsynligheden for hvert terningslag.

Der er i alt 36 kombinationer. Slår vi en 1'er med terning 1, er der 6 forskellige kombinationer med terning 2. Slår vi en 2'er med terning 1 er der igen 6 forskellige muligheder med terning 2. Og så videre. I alt 36 muligheder.

Så sådan set er det jo nemt nok. Men der er et par faldgruber.

 

Figur 2

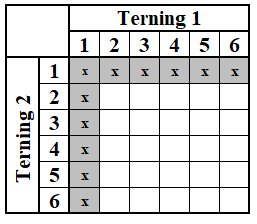
I figur 2 er vist alle de forskellige muligheder for at rulle en 1'er. Vi kan rulle en 1'er med terning 1 og et vilkårligt slag med terning 2. I alt 6 muligheder. Eller vi kan rulle en 1'er med terning 2 og et vilkårligt slag med terning 1. Men nu er der kun 5 ekstra muligheder. Slaget, hvor begge terninger viser 1 (pas et eller dobbelt et), har vi jo allerede talt med. Så derfor er der i alt 11 muligheder for at rulle en 1'er, når vi slår med 2 terninger.

 

Figur 3

I figur 3 er hvid på baren, og sort har et 5-punkts-bord. Hvid skal rulle en 5'er for at komme ind fra baren. Det sker 11 ud af 36 gange. Sandsynligheden er 11/36 = 30,6 %. Det er nyttigt at huske, at hvid her har 11 numre, der kommer ind, og at det svarer til ca. 30 %, hvis man i farten ikke lige kan regne ud, hvad 11 divideret med 36 er!

 

Figur 4

I figur 4 skal hvid rulle en 1'er for at have en chance for at vinde partiet. Igen er der 11 ud af 36 muligheder.

 

Figur 5

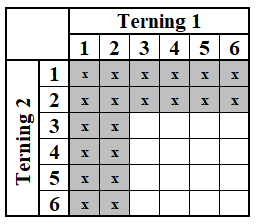
Hvad så, når vi har brug for at rulle ét af 2 specifikke numre, for eksempel en 1'er eller en 2'er? Kombinationerne er vist i figur 5. Der er i alt 20 muligheder. Først de 11 muligheder for at rulle en 1'er. Derefter yderligere de 9 muligheder for at rulle en 2'er, hvor den anden terning ikke er en 1'er (som jo allerede er talt).

Det bliver vi også nødt til at kunne huske. Enten skal vi huske, at der er 20 muligheder for at slå ét ud af to numre, eller at der er 11 muligheder for at rulle det første nummer efterfulgt af 9 muligheder for at rulle det andet nummer, altså:

• 11 – 20, eller
• 11 – 9.

Sandsynligheden er 20/36 eller ca. 55½ %.

 

Figur 6

I figur 6 er hvid på baren mod et 4-punkts-bord. Hvid skal bruge en 1'er eller en 5'er for at komme ind. Sandsynligheden er 20/36 = ca. 55½ %. Hvid er favorit til at komme ind.

 

Figur 7

I figur 7 skal hvid bruge en 1'er eller en 2'er for at have en chance for at vinde partiet. Igen er sandsynligheden 20/36 = 55½ %.

 

Figur 8

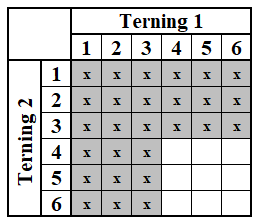
Har vi brug for at rulle ét ud af 3 specifikke numre, er der nu 7 yderligere muligheder, dvs. at der i alt er 27 ud af 36 muligheder for at rulle ét af de tre numre, det vi sige 75 %. Omvendt er der 25 % chance for ikke at rulle et af de 3 numre.

Dvs. at vi 75 % chance for at rulle en 1'er eller en 2'er eller en 3'er – eller for den sags skyld – 75 % chance for at rulle en 2'er eller en 4'er eller en 6'er. Når vi har brug for ét ud af 3 specifikke numre er sandsynligheden 75 %.

Nu bliver vores talrække:

• 11 – 9 – 7, eller
• 11 – 20 – 27.

Igen er det ligegyldigt, hvilken af talrækkerne, vi memorerer. Det er blot vigtigt at huske én af dem.

Vi behøver ikke at se flere eksempler. Hvis vi fortsætter, bliver talrækkerne til:

• 11 – 9 – 7 – 5 – 3 – 1, eller
• 11 – 20 – 27 – 32 – 35 – 36.

 

Sammensatte sandsynligheder

 

Lad os nu se på nogle kombinationsmuligheder:

 

Figur 9

I figur 9 skal hvid rykke en 1'er. Skal hvid blive stående på 13-punktet eller rykke frem til 12-punktet? Hvid skal blot sørge for ikke at blive ramt. Lykkes det, har hvid meget store chancer for at vinde partiet.

Vi bliver nødt til at tælle for at finde svaret. Vi kan ræsonnere som følger:

Uanset om hvid bliver stående på 13-punktet eller rykker frem til 12-punktet, er der 11 numre, der rammer direkte (alle 6’ere eller alle 5’ere). Det er det samme, så det kan vi se bort fra. Vi skal derfor finde de ekstra numre:

 

Figur 10 – Hvid bliver stående

 

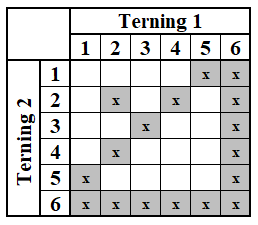
Figur 11 – Hvid rykker til 12-punktet

 

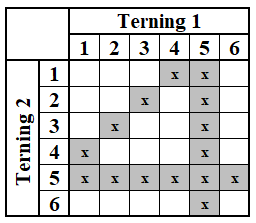
I figur 10 kan vi se, at hvis hvid bliver stående, er der 6 ekstra numre, der rammer ud over de 11 seksere, dvs. i alt 17 numre ud af 36. Rykker hvid frem til 12-punktet, er der kun 4 ekstra numre ud over 5'erne, dvs. i alt 15 numre ud af 36, som vi ser i figur 11.

Hvid ”sparer” altså 2 numre ved at rykke frem. Det er næsten 6 % gevinstchance (=2/36). Det er meget i backgammon.

Bliver vi ved, kan vi hurtigt se, at jo tættere 2 brikker står på hinanden, des mindre risiko er der for at blive ramt.

 

Figur 12

 

Figur 13

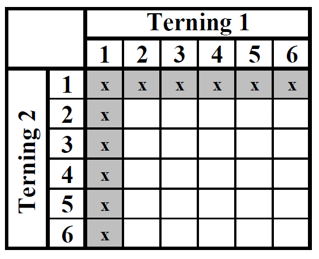
I figur 12 har hvid kun 1'ere, der rammer sort, dvs. 11 numre (figur 13).

 

Figur 14 

 

Figur 15

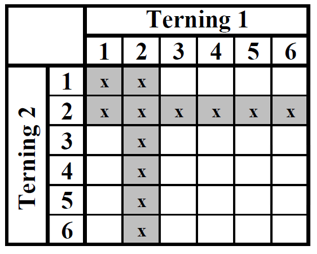
I figur 14 har hvid 2'ere plus pas 1 (11), der rammer, dvs. i alt 12 numre (figur 15).

 

Figur 16 

 

Figur 17

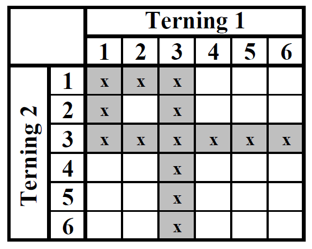
I figur 16 har hvid alle 3'ere plus 21 og pas 1, der rammer, dvs. 14 numre (figur 17).

 

Figur 18 

 

Figur 19

 

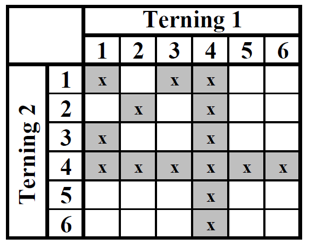
I figur 18 har hvid 15 numre, der rammer (figur 19).

Har vores modstander et direkte skud, og vi har brug for at minimere antallet af skud, er der derfor ikke noget at betænke sig på: Brikken skal flyttes så tæt på modstanderen som muligt.

Det omvendte gælder, hvis vores modstander kun har et indirekte skud:

Figur 20

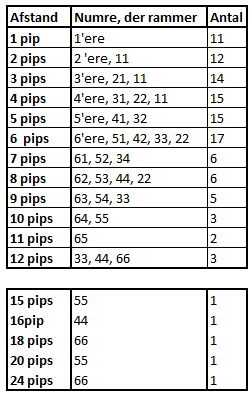
Er der ingen direkte skud, er det sikrest at være så langt væk som muligt, bortset fra, at det er lidt sikrere at være 11 pips væk end 2 pips væk, som vi kan se i figur 20.  Farligst er det at være 7 eller 8 pips væk. I begge tilfælde har modstanderen 6 numre, der hitter (hvis der ikke er blokeringer undervejs). Bedst er det at stå så langt væk, at kun de store dobbeltslag giver skud. Ulempen er dog, at jo længere væk vores brik står, des sværere er det at få den  bragt i sikkerhed, som vi kan se i næste figur.

 

Figur 21

Ofte kan det betale sig at tænke fremad. I figur 21 skal hvid rykke 21. Det er klart, at hvid ikke ønsker at rykke 2'eren fra 15-til 13-punktet, da giver alt for mange direkte skud. Men hvad med 1'eren? Skal den den hvide brik stå 7 eller 8 pips væk fra sort?

Vi ved fra figur 20 (eller fordi vi har talt efter), at hvids risiko for at blive ramt er lige stor, hvad enten den hvide brik er 7 eller 8 pips væk fra de sorte brikker på 7-punktet (sort har 6 muligheder for at rulle en 7’er og 6 muligheder for at rulle en 8’er). Så spørgsmålet er, hvad situationen vil være i næste rul. Hvis hvid bliver stående, har hvid 11 slag, der bringer den sidste brik i sikkerhed næste gang (66, 65, 64, 63, 55, 54 og 33). Rykker hvid brikken frem til 14-punktet er der hele 16 slag, der bringer brikken i sikkSuoperhed i næste rul (66, 65, 64, 63, 62, 55, 54, 53, 44, 33). Så det er altså bedst at rykke 15/14 med 1’eren.

Det er et lidt besværligt regnestykke, men det er præcis den måde at tænke på, som gør det muligt at optimere spillet, dvs. at øge chancerne for, at der sker noget godt i næste rul.

 

Figur 22

I figur 22 skal hvid igen rykke 21 og igen er spørgsmålet, hvordan etteren skal rykkes. Før skulle den rykkes 15/14. Men er det stadig rigtigt?

Nej, for nu er sorts 22’ere og 44’ere blokeret. Sort har derfor nu kun 4 gode 8’ere, men stadig 6 gode 7’ere. Så nu gælder det om at blive tilbage for hvid. Hvid må derfor rykke både 1'eren og 2'eren inde i bordet.

Hele tiden bør vi huske at tælle efter. Princippet er ikke så vanskeligt, men det kan tage noget tid at vænne sig til.

 

Figur 23

I figur 23 (som vi har lånt fra Walter Trice's ”Backgammon Boot Camp”, s. 65) skal hvid rykke 54 og er tvunget til at flytte mindst én brik fra 18-punktet. Skal hvid rykke 18/9 eller 18/14 18/13? Hvid kommer til at give dobbeltskud i begge tilfælde.

 

Figur 24

 

Figur 25

Vi kan finde svaret ved at tælle numre. Men nu kan vi også finde svaret uden at tælle! For det første ved vi, at ved at rykke 18/14 18/13 får sort 20 numre, der hitter (figur 24). Og hvordan ved vi det? Det ved vi, fordi sort skal rulle enten en etter eller en toer for at hitte en hvid brik. 11 hitter begge brikker, men det er ligegyldigt. Der er ingen ekstranumre, der hitter.

Rykker hvid 18/9 er der også 20 hitnumre (alle seksere og ettere). Men herudover er der nogle kombinationer, fx 42, der også hitter. Så i figur 25 er der mere end 20 numre, der hitter. Det afgør sagen, og hvid rykker 18/14 18/13.

 

Bestemte kombinationer

 

Figur 26

I figur 21 har sort blitzet med 55 og sendt 2 hvide brikker på baren. Hvad er sandsynligheden for, at hvid kommer ind med en af brikkerne i næste rul? Det ved vi godt: Det er 27/36 = 75 %.

Men hvad er sandsynligheden for, at hvid kommer ind med begge brikker i næste rul? Igen kan vi tælle op:

Der er de 3 dobbeltslag. Desuden er der 54, 52 og 42. I alt 9 slag, så sandsynligheden er 25 % (9/36). Det vidste vi sådan set godt, for sandsynligheden for ikke at komme ind med begge brikker er den samme som sandsynligheden for enten at rulle 1, 3 eller 6. Altså er sandsynligheden for ikke at komme ind med begge brikker 75 % – og derfor er sandsynligheden for at komme ind med begge brikker 25 %.

Hvis vi ikke gider at tælle hver gang, vi har brug det (og det er tit!), kan vi benytte følgende genvej:

 

Figur 27

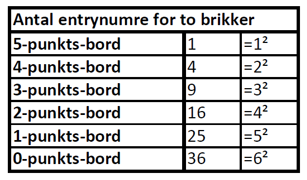
Vi kan tage antallet af tomme punkter i bordet og gange tallet med sig selv! Vi har lige set, at der er 9 numre, der bringer 2 mand ind fra baren mod et 3-punkts-bord. Det er det samme som 3².

Mod et 2-punkts-bord er der 4 tomme punkter, hvilket giver 16 "entrynumre" (4²). Og så videre. Den er god nok, tæl selv efter.

Den samme tankegang, kan vi bruge, når vi skal bygge et bestemt punkt (og her er det endnu mere nyttigt).

 

Figur 28

Hvad er sandsynligheden for, at hvid i figur 28 kan lave 5-punktet? Det er ret let at se: Hvid kan bruge 21, 22 og 11, i alt 4 numre. Men vi kan også sige det sådan: Hvid har byggere på 2 punkter: Det giver 2² muligheder for at lave et bestemt punkt. Det er den samme logik som før.

 

Figur 29

I figur 29 vil hvid gerne lave 4-punktet. Hvad er sandsynligheden? Hvid kan bruge 32, 31, 21 og 33, 22 og 11, i alt 9 numre. Det er det samme som 3².

Det ser ud til at mønstrene går igen. Har hvid byggere på 4 punkter, er der 16 eller 4² muligheder for at lave et bestemt punkt. Vi kan bruge teknikken til hurtigt at danne os et overblik over mulighederne:

 

Figur 30

I figur 30 vil hvid gerne bygge en fuld 6-prime. Hvid skal altså bygge 5-punktet uden at bryde nogle af de andre punkter. Med regnereglen om kvadrater går det hurtigt:

Hvid har ekstra byggere på 4 punkter. 5-punktet kan altså bygges på 16 forskellige måder (4²), men 55 og 44 dur ikke, for de laver ikke den fulde prime

Så hvid har 14 muligheder for at lave en fuld 6-prime. 22/36 er godt 60 %. Ikke ringe. Men det vigtige er, at vi i stedet for at tælle kombinationerne (54, 52, 51, 42, 41, 21, 22 og 11) bruger en hurtig genvej til samme resultat.

Endnu hurtigere går det, hvis vi blot vil vide, hvor mange numre der laver 5-punktet. Der er byggere på 5 punkter, så det er 5² = 25 muligheder. Eller sagt på en anden måde: Det er kun rul indeholdende 6’ere, der ikke laver punktet. Dem er der 11 af. Så der må være 36 – 11 = 25 muligheder for at lave punktet.

Der er ingen vej uden om at vænne sig til at tælle kombinationer. Hen ad vejen kommer det til at sidde fast, og når det kombineres med de genveje, som er beskrevet i denne lektion, kommer det efterhånden til at gå hurtigt.

 

Andre kombinationer

 

Figur 31

I figur 31 skal hvid rykke 41. Sort har lukket bordet, så det gælder om at minimere antallet af skud. Bemærk den sorte brik på baren. 

Spørgsmålet er: Skal vi rykke en brik til 2-punktet eller hitte den sorte brik på 1-punktet?

Igen må vi tælle: Hitter vi på 1-punktet, er der 11 numre, der rammer (alle 1’erne). Spiller vi i stedet 7/2, er der 11 2'ere, der rammer, plus 41, 31 og 11, altså 5 yderligere numre, hvilket i alt giver 16 numre. Hvid er derfor nødt til at hitte på 1-punktet og håbe på, at sort ikke ruller en 1'er, og at den hvide brik kan dækkes næste gang.

 

Figur 32

Når vi kommer til udtagningen, er det især vigtigt at have styr på kombinationerne. I figur 32 skal hvid rykke en 1’er. Der er to muligheder: 6/5 og 2/1.

Hvids eneste mulighed for at vinde er, at sort ikke slår et dobbeltslag og derefter at få begge brikker af i næste rul. Så vi kan tælle hvids gode rul, hvis hvid flytter 2/1: Hvid tager 2 brikker af med alle 6’ere (det er 11 numre) plus 55, 44, 33 og 22. Det er 15 numre i alt.

Hvis hvid i stedet flytter 6/5, så giver det 9 gode 6’ere (alle 6’ere på nær 61) og dertil 7 gode 5’ere (alle 5’ere på nær 51 og 56, som allerede er talt). Så er vi allerede oppe på 16 og behøver ikke at tælle videre. Gør vi det alligevel, er det let at se, at 44, 33 og 22 også tager begge brikker af. I alt har hvid hermed 19 gode numre. Det rigtige er altså at flytte 1’eren fra 6-punktet til 5-punktet.

 

Figur 33

I figur 33 skal hvid igen flytte en 1'er og skal sørge for at maksimere sandsynligheden for at få begge brikker af i næste rul.

Hvis hvid rykker 2/1 har hvid følgende gode rul næste gang: 11 6’ere og 9 5’ere, plus 44, 33, 22, i alt 23 numre.

Hvis hvid rykker 5/4, er der følgende gode rul: 9 6’ere, 7 5’ere og 5 4’ere, plus 33 og 22, i alt 23 numre.

De to ryk er lige gode.

 

Figur 34

 

I figur 34 skal hvid igen rykke en 1'er. Vi ved allerede (fra figur 32), at hvis hvid rykker 3/2, så har hvid 19 gode numre næste gang.

Rykker hvid 5/4 kan vi tælle: 7 gode 6’ere, 5 gode 5’ere og 3 gode 4’ere plus 33 og 22. I alt 17 numre. Så hvid skal rykke 3/2.

Som det har vist sig, så har det særligt i udtagningen overordentlig stor betydning for vinderchancerne, at vi formår at tælle kombinationerne korrekt.

 

Opsummering

I backgammon drejer beregning af sandsynligheder mest af alt om at tælle. Hitnumre, "dansenumre" (numre, hvor man ikke kan komme ind fra baren), entrynumre, kombinationsmuligheder og meget mere. Husk at tælle både de direkte numre, de indirekte numre og kombinationerne.

 

læs mere

• Walter Trice: “Backgammon Boot Camp”, kap. 8: Blots, Odds And Shots
• Marc Olsen: ”Backgammon – Fra basics til badass”, kap. 4: ”Terningekombinatorik”
• Paul Magriel, ”Backgammon”, kap.11: Basic Odds

 

Akademiets forside | Opgaver til lektion 3 | Video til lektion 3 – del 1 |  Video til lektion 3 – del 2  | Video til lektion 3 – del 3 | Lektion 4